Pi

Kitos reikšmės – Pi (reikšmės).

Graikų abėcėlės raidė pi

π (tariama pi, nuo gr. περίμετρος – „perimetras“, turima omenyje apskritimo perimetras) – matematinė konstanta, plačiai naudojama matematikoje ir fizikoje. Jos žymėjimui naudojama graikiška raidė pi.

$\pi\approx 3{,}141592654$

Euklido geometrijoje π naudojama apskritimo perimetrui bei plotui paskaičiuoti. Daugumoje naujesnių knygų π analitiškai apibrėžiama trigonometrinėmis funkcijomis, t. y. kaip mažiausią teigiamą x, kuriam sin(x) = 0.
π yra Iracionalusis skaičius, taip pat nenustatyta ar yra kokia nors seka jo užrašymui, apytikslė šio skaičiaus reikšmė yra:

3,141 592 653 589 793 238 462 643 383 279 502 884 197 169 399 375 105 820 974 944 592 3

Tikslesnę π išraišką galima rasti – Pi reikšmė (100 000 skaitmenų). Pi reikšmė failais (5 trilijonai skaitmenų).

Savybės

Apskritimo ilgio ir skersmens santykis – π

Pi yra iracionalusis skaičius, tai yra negali būti užrašytas kaip dviejų sveikųjų skaičių santykis. Tai 1761 metais įrodė Johanas Heinrichas Lambertas (Johann Heinrich Lambert). 1882 metais įrodyta, kad skaičius yra transcendentinis, tai yra neegzistuoja toks daugianaris su racionaliais koeficientais, kurio šaknis būtų π.
Tuo pačiu neįmanoma išreikšti π reikšmės naudojant baigtinį kiekį sveikų ir racionalių skaičių bei jų šaknų. Tai reiškia, kad neįmanoma naudojant liniuotę ir skriestuvą nupiešti kvadrato, kurio plotas būtų lygus duoto apskritimo plotui.

Formulės su π

Geometrija

Pi naudojama daugelyje geometrinių formulių, susijusių su apskritimais ir sferomis.

Geometrinė figūra	Formulė
Apskritimo ilgis (spindulys – r)	$C = 2 \pi r \,\!$
Skritulio plotas (spindulys – r)	$S = \pi r^2 \,\!$
Elipsės plotas (pusašiai a ir b)	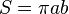$S = \pi a b \,\!$
Sferos tūris (spindulys – r)	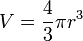$V = \frac{4}{3} \pi r^3 \,\!$
Sferos paviršiaus plotas (spindulys – r)	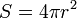$S = 4 \pi r^2 \,\!$
Cilindro tūris (aukštis h, spindulys r)	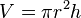$V = \pi r^2 h \,\!$
Cilindro paviršiaus plotas (aukštis h, spindulys r)	$S = 2 ( \pi r^2 ) + ( 2 \pi r ) h = 2 \pi r (r + h) \,\!$
Kūgio tūris (aukštis h, spindulys r)	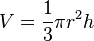$V = \frac{1}{3} \pi r^2 h \,\!$
Kūgio paviršiaus plotas (aukštis h, spindulys r)	$S = \pi r \sqrt{r^2 + h^2} + \pi r^2 = \pi r (r + \sqrt{r^2 + h^2}) \,\!$

Taip pat 180° (laipsniais) kampas yra lygus π radianų.

Analizė

Daugelis matematinės analizės formulių naudoja π, įskaitant begalines progresijas (ir baigtines sandaugas), integralus ir specialiąsias funkcijas.

François Viète, 1593:

$\frac2\pi= \frac{\sqrt2}2 \frac{\sqrt{2+\sqrt2}}2 \frac{\sqrt{2+\sqrt{2+\sqrt2}}}2\ldots$

Leibnico formulė:

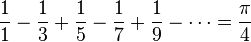
$\frac{1}{1} - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \frac{1}{9} - \cdots = \frac{\pi}{4}$

Tai dažniau pasitaikantis užrašymas, bet formalesnis užrašymas yra:

$\sum_{n=0}^{\infty} (-1)^{n} \left (\frac{1}{2n+1}\right ) = \frac{\pi}{4}$

Valio sandauga:

$\frac{2}{1} \cdot \frac{2}{3} \cdot \frac{4}{3} \cdot \frac{4}{5} \cdot \frac{6}{5} \cdot \frac{6}{7} \cdot \frac{8}{7} \cdot \frac{8}{9} \cdots = \frac{\pi}{2}$

Atviri klausimai

Svarbiausias su π susijęs neatsakytas klausimas – ar tai normalusis skaičius, t. y. ar egzistuoja kokia nors nuspėjama skaitmenų seka ar kiekvienas tolesnis skaitmuo visai „atsitiktinis“. Tai galiotų ne tik dešimtainei sistemai. Dabartinės žinios yra pakankamai mažos – net nežinoma, kuris iš skaitmenų pasitaiko be galo dažnai.
Taip pat nežinoma ar π ir e yra algebriškai nepriklausomos konstantos, t. y. ar egzistuoja polinominis ryšys tarp π ir e su racionaliaisiais koeficientais.

π prigimtis

Ne Euklido geometrijoje trikampio kampų suma gali būti didesnė ar mažesnė už π radianų, taip pat apskritimo ilgio ir spindulio santykis gali būti nelygus π. Tačiau tai nekeičia π apibrėžimo, tik formules, kuriose naudojama π. Taigi, π reikšmei neturi įtakos visatos forma, ji nėra fizikinė, bet matematinė konstanta, apibrėžta nepriklausomai nuo bet kokių fizikinių matavimų. Ji naudojama ir fizikoje tik todėl, kad yra patogi daugumoje modelių.

Categories

Archives

Nuorodos

Pi